Stepping into the Cosmos: Building an N-Body Gravity Simulator

What happens when multiple celestial bodies interact under the force of gravity? Can we simulate the complex and chaotic motion of planets, stars, and galaxies in a computational environment?

This week's Project52 experiment takes a deep dive into gravitational interactions with an interactive, real-time N-Body Gravity Simulation, coded from scratch using C, OpenGL, and GLFW.

But this isn't just another physics-based visualization—this project was built as a tool for experimentation, learning, and exploration, allowing me to interact, modify, and observe how celestial objects move, and form complex orbital dynamics.

🧑‍🚀 Why Build an N-Body Simulator?

The N-Body Problem is a classic problem in physics, describing the motion of multiple interacting objects under mutual gravitational influence. Unlike simple two-body systems like the Earth and Moon, an N-body system cannot be solved analytically due to the chaotic nature of the interactions. Instead, we rely on numerical methods and simulations to predict motion.

This project started as an experiment to simulate gravitational dynamics in real-time, allowing me to:

✅ Observe stable orbits, chaotic interactions, and emergent patterns
✅ Add new bodies dynamically and see how randomized mass & velocity affect the system
✅ Experiment with 2-body, 3-body, and solar system-like setups
✅ Use real-time OpenGL rendering to display trails, camera movement, and object interactions

But getting this to work wasn’t easy. The simulation had to balance accuracy, performance, and interactivity, all while being visually engaging.

Interactivity in the N-Body Gravity Simulator: A Key Feature

One of the standout aspects of this N-Body Gravity Simulator is its interactive nature, which transforms it from a mere visualization tool into a hands-on experimental playground for celestial mechanics. The ability to modify the simulation in real time allows me to observe gravitational dynamics as they unfold, adjust parameters on the fly, and create unique scenarios that showcase the beauty and complexity of multi-body interactions.

🌟 Why Interactivity Matters

• Real-Time Experimentation – Instead of running pre-determined simulations, I can create their own scenarios and study emergent behaviors.

• Understanding Orbital Mechanics – The ability to manipulate variables such as time scale, number of bodies, and initial conditions helps me understand concepts like Lagrange points, gravitational slingshots, and chaotic trajectories.

• Observing the Butterfly Effect – Small changes can have drastic long-term consequences in multi-body systems, and real-time interactivity lets me explore how minor tweaks affect the system.

⚙️ Technology Stack & Simulation Details

This project is built using:

• C – for performance and fine-grained memory management.

• OpenGL & GLFW – for high-performance rendering of celestial bodies.

• GLEW – for OpenGL extensions.

• Physics Engine – Custom physics using Newtonian Gravity with Euler Integration.

• User Interactivity – Building an interactive physics simulation required a combination of real-time input handling, rendering optimizations, and physics calculations. Here’s how it was achieved:

  1️⃣ Real-Time Input Handling – GLFW & Keyboard/Mouse Controls

  • GLFW was used for keyboard and mouse input processing, allowing users to:

    • Pause/unpause the simulation (Spacebar).

    • Adjust the time scale (+ and - keys).

    • Add new celestial bodies with randomized mass and velocity (A key).

    • Remove specific bodies (D key).

    • Toggle and clear gravitational trails (T and C keys).

    • Switch between different preset scenarios (1-4 keys).

    • Reset the camera (R key).

  2️⃣ Dynamic Camera System – Mouse-Controlled 3D Navigation

  • Free-roam camera movement was implemented to allow users to explore the system from any angle.

  • Camera controls:

    • Rotate the view by dragging the mouse.

    • Zoom in and out using the scroll wheel.

    • Click to select individual celestial bodies, making them easier to track.

  3️⃣ OpenGL Rendering – Smooth & Scalable Performance

  • OpenGL shaders were used to efficiently render bodies and their trails, ensuring smooth performance even with a large number of objects.

  • The system dynamically updates:

    • Object positions.

    • Motion trails to track each body's past trajectory.

    • Lighting and shading to create a realistic depth effect.

🔢 The Physics Behind the Simulation

At the core of the simulation is Newton’s Law of Universal Gravitation:

Where:

• F is the gravitational force

• G is the gravitational constant (6.674 × 10⁻¹¹ N·m²/kg²)

• m₁, m₂ are the masses of the two bodies

• r is the distance between them

Each frame, the acceleration of each body is computed using:

Then, we update velocity and position using Euler integration:

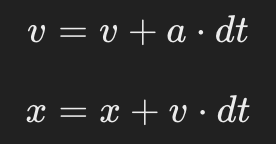
where dt is the simulation timestep.

🖥️ OpenGL Rendering

The visualization uses OpenGL to:

• Render spheres for celestial bodies using VAOs and VBOs

• Draw motion trails to visualize past trajectories

• Provide an interactive camera that allows panning, zooming, and rotation

Each body is drawn as a 3D sphere with realistic shading, while trails are rendered as line strips for historical motion tracking.

🌀 The Simulated Scenarios

The video showcases multiple gravitational setups:

1️⃣ Two-Body Simulation (Binary System)

• The simplest case: Two objects orbiting each other due to mutual gravitational attraction.

• Used to test stability and validate Newtonian gravity equations.

• Demonstrates how orbital dynamics emerge from just two interacting masses.

2️⃣ Three-Body Problem

• Introduces a third object to the mix.

• Unlike two-body motion, three-body motion is highly chaotic.

• Shows Lagrange points, collisions, or objects being ejected.

3️⃣ Solar System-Like Setup

• A massive central object (representing a star or black hole).

• Several smaller bodies orbiting around it.

• Used to test planetary system stability and orbital resonances.

4️⃣ Full N-Body System (User-Generated Chaos)

• Pressing A dynamically spawns a new body with random mass, velocity, and position.

• Over time, the system evolves into a chaotic N-body system.

• Some objects collide and merge, while others get ejected.

• The most massive objects tend to dominate, mimicking real astrophysical behavior.

💡 Challenges & Solutions

1️⃣ Performance Issues

• N-body simulations scale as O(N²) due to pairwise force calculations.

• Solution: Optimized memory layout and efficient loop structures.

2️⃣ Numerical Instability

• Euler integration sometimes caused orbits to decay or explode.

• Solution: Clamped time step and velocity scaling to ensure stable physics.

3️⃣ Camera & Rendering

• Needed fluid camera movement without jitter.

• Solution: Implemented quaternion-based camera rotation.

🚀 What's Next?

This experiment has opened new doors for expansion:

🔹 GPU Acceleration: Using OpenCL or CUDA for parallelized force computations.
🔹 Better Physics Integration: Switch from Euler to Verlet or Runge-Kutta methods.
🔹 User-Defined Systems: Load predefined galaxy structures or custom orbital parameters.
🔹 Black Holes & Relativity: Add general relativistic corrections for high-mass objects.

📌 Final Thoughts

This week’s Project52 experiment was a deep dive into astrophysical simulation, real-time physics, and performance optimization.

By coding an interactive, real-time universe, we not only pushed technical boundaries but also gained insights into real-world orbital mechanics.